天泣記

2020-07-18 (Sat)

#1 有理数を循環小数に変換する

ふと、有理数 n/d を循環小数に変換するメソッドを書いてみた

これを行うには、x_{i+1} = (10 * x_i) % d という漸化式で 定義される数列が、どこで cycle するかを検出しなければならない

x_i は d 未満の非負整数なので、状態数が有限であるため、かならずどこかで cycle が起きる

なお、数列の最初のあたりは cycle にならないことがある

x_0 から x_{h-1} は cycle に含まれず、 x_h から x_{h+l-1} が最初の cycle とすると、 h と l を求める、というのが cycle を検出する、という話である

これを行うにはいくつかのアルゴリズムがあるが、 wikipedia の Cycle detection にのっている、 兎と亀のアルゴリズム、 Brent のアルゴリズム、 Gosper のアルゴリズムというのを使って実装してみた

なお、Hare というのが野うさぎらしい (亀は Tortoise)

兎と亀のアルゴリズムおよび Brent のアルゴリズムは実行中に数列の要素を 2つしか保持しないのに対し、 Gosper のアルゴリズムは log くらいの要素を保持する。 たくさん保持するぶん、cycle を速やかに検出することが期待されるので速いのではないかと思ったのだが... 後述

# recurring-decimal.rb
class Rational
  # uses Floyd's Tortoise and Hare
  def to_dec_th
    sign = self < 0 ? "-" : ""
    n = self.numerator.abs
    d = self.denominator
    int, mod = n.divmod(d)
    s = "#{sign}#{int}"
    return s if mod == 0

    # There are fractional digits.
    #
    # If the fractional digits is recurring,
    # it begins with non-recurring part of length h and
    # recurring part of length l.
    # foobarbazbazbaz... = foobar(baz) : h = 6, l = 3
    #
    # We have a sequence
    # x0 = mod
    # x1 = (x0 * 10) % d
    # ...
    # x{i+1} = (xi * 10) % d
    # ...
    #
    # Since this sequence repeats from xh,
    # xj = x{j+k*l} for all j >= h and k >= 0.

    # At first, we find some i such that xi = x{2i}.
    # However, we don't use i itself.
    # i = 0
    m1 = m2 = mod
    begin
      m1 = (m1 * 10) % d
      # i += 1
      m2 = (m2 * 10) % d
      m2 = (m2 * 10) % d
    end while m1 != m2
    # We found i such that xi = x{2i}
    # The difference of i and 2i is a multiple of the cycle length, l.
    # 2i - i = i = k * l for some k.

    # Then, we detect h.
    # We search h from 0 to detect xh = x{h+k*l} = x{h+i}.
    f = ""
    h = 0
    m1 = mod
    while m1 != m2
      d1, m1 = (m1 * 10).divmod(d)
      f << d1.to_s
      m2 = (m2 * 10) % d
      h += 1
    end

    # If m2 is zero, the number is not recurring.
    return "#{s}.#{f}" if m2 == 0

    # At last, we find the recurring part.
    l = 0
    f << "("
    m2 = m1
    begin
      d1, m1 = (m1 * 10).divmod(d)
      f << d1.to_s
      l += 1
    end while m1 != m2
    f << ")"

    "#{s}.#{f}"
  end

  # uses Gosper's loop detector
  def to_dec_gosper
    sign = self < 0 ? "-" : ""
    n = self.numerator.abs
    d = self.denominator
    int, mod = n.divmod(d)
    s = "#{sign}#{int}"
    return s if mod == 0

    f = ""

    # Gosper's loop detector
    # https://web.archive.org/web/20160414011322/http://hackersdelight.org/hdcodetxt/loopdet.c.txt
    x0 = mod
    ms = [x0]
    x = x0
    n = 1
    while true
      digit, x = (x * 10).divmod(d)
      f << digit.to_s
      return "#{s}.#{f}" if x == 0
      break if k = ms.index(x)
      n +=1
      j = (n & ~(n - 1)).bit_length - 1
      ms[j] = x
    end
    m = ((((n >> k) - 1) | 1) << k) - 1;
    l = n - m;
    lgl = (l - 1).bit_length - 1
    h_lo = m - [1, 1 << lgl].max + 1;
    # Now, we have the length of the recurring part, l, and
    # a lower bound of the length of the non-recurring part, h_lo.

    # find the exact length of the non-recurring part, h.

    # At first, find an element before the recurring part.
    # Any element works well but we find maximum one already computed.
    m0 = nil
    k0 = nil
    ms.each_index {|k2|
      m2 = ((((n >> k2) - 1) | 1) << k2) - 1;
      next if h_lo < m2
      if m0 == nil || m0 < m2 then
        k0 = k2
        m0 = m2
      end
    }
    if m0 then
      h = m0
      x1 = ms[k0]
    else
      h = 0
      x1 = x0
    end

    # advance l times
    x2 = x1
    l.times {
      x2 = (x2 * 10) % d
    }

    # find h.
    while x1 != x2
      h += 1
      x1 = (x1 * 10) % d
      x2 = (x2 * 10) % d
    end

    "#{s}.#{f[0, h]}(#{f[h,l]})"
  end
end

# References:
# * Cycle detection
#   https://en.wikipedia.org/wiki/Cycle_detection
# * HAKMEM ITEM 132 (Gosper): LOOP DETECTOR
#   http://www.inwap.com/pdp10/hbaker/hakmem/flows.html
# * Gosper's loop detector implementation
#   https://web.archive.org/web/20160414011322/http://hackersdelight.org/hdcodetxt/loopdet.c.txt

これを使うと、以下のように、有理数を十進の循環小数に 変換して、循環部分を括弧で括った文字列を得られる

(1/3r).to_dec_th #=> "0.(3)"
(1/7r).to_dec_th #=> "0.(142857)"
(22/7r).to_dec_th #=> "3.(142857)"
(27/88r).to_dec_th #=> "0.306(81)"

循環しない小数で表現可能なら、括弧の部分はつかないようにしてある (0 が循環するとして "(0)" をつけてもいいのだが)

(1/5r).to_dec_th #=> "0.2"

とりあえず、以下のようにして 3個のメソッドが同じ結果になることを確認した (なんとなく、各分母に対して分子は乱数にしてみた)

% ruby -r./recurring-decimal.rb -e '
1.upto(20000) {|i|
  r = rand(i).to_r/i
  s1 = r.to_dec_th
  s2 = r.to_dec_brent
  s3 = r.to_dec_gosper
  raise if s1 != s2 || s1 != s3
}
'

せっかく同じ動作をするメソッドを 3個も実装したので、 速度を測ってみよう

まずは平均から

% ruby -r./recurring-decimal.rb -e '
acc_a, acc_b, acc_c = 0.0, 0.0, 0.0
n = 2000
1.upto(n) {|i|
  r = rand(i).to_r/i
  t1 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s1 = r.to_dec_th
  t2 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s2 = r.to_dec_brent
  t3 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s3 = r.to_dec_gosper
  t4 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  acc_a += t2 - t1
  acc_b += t3 - t2
  acc_c += t4 - t3
}
printf("to_dec_th:     %f\n", acc_a / n)
printf("to_dec_brent:  %f\n", acc_b / n)
printf("to_dec_gosper: %f\n", acc_c / n)
'
to_dec_th:     0.000224
to_dec_brent:  0.000281
to_dec_gosper: 0.000567

うぅむ、いちばん素朴な兎と亀のアルゴリズムを使ったもの (to_dec_th) がいちばん速くて、 いちばん凝った Gosper のアルゴリズムを使ったもの (to_dec_gosper) がいちばん遅い

生データをとってプロットしてみよう

% ruby -r./recurring-decimal.rb -e '
acc_a, acc_b, acc_c = 0.0, 0.0, 0.0
n = 2000
puts "numerator,t,alg\n"
1.upto(n) {|i|
  r = rand(i).to_r/i
  t1 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s1 = r.to_dec_th
  t2 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s2 = r.to_dec_brent
  t3 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s3 = r.to_dec_gosper
  t4 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  a = t2 - t1
  b = t3 - t2
  c = t4 - t3
  printf "%d,%g,th\n", i, a
  printf "%d,%g,brent\n", i, b
  printf "%d,%g,gosper\n", i, c
}
' > recurring-decimal.csv

recurring-decimal.R:

library(ggplot2)
d <- read.csv("2020-07/recurring-decimal.csv")
p <- ggplot(d, aes(numerator, t)) +
  geom_point(aes(colour = alg)) +
  ylab("t[s]")
print(p)

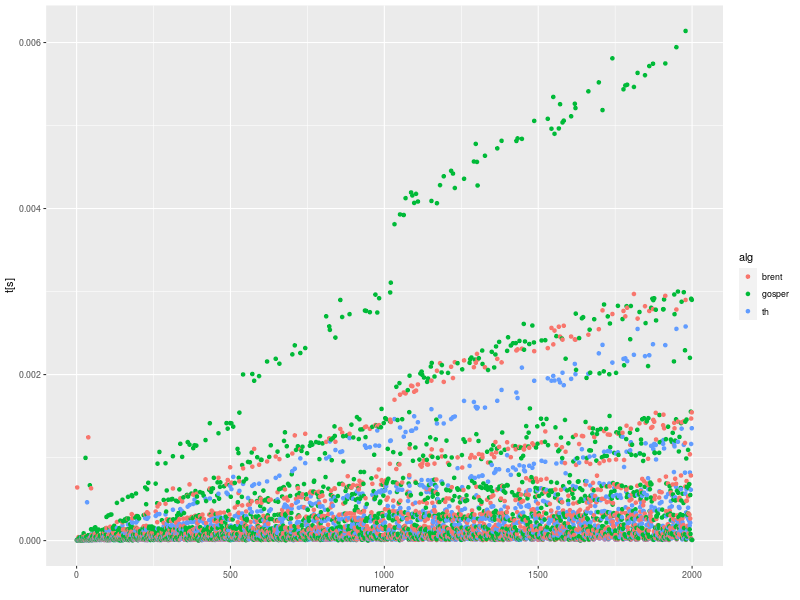
recurring-decimal.png

三角形になっているのは、 分母が大きくなるほど小数点以下の桁数が長くなる可能性がある (分子によっては短くなることもある) のでそれはそうなるか、という感じ

時間がかかっているのは、to_dec_gosper が多くて、 次いで to_dec_brent が多い、 というのは平均と整合する

ということで、循環小数については難しいことはせず、素朴に兎と亀のアルゴリズムを使うのがよさそう

#2 Gosper の loop detector

Gosper の loop detector は、 数列を最初から順に調べていき、 いくつかの (調べた範囲の log くらいの) 要素を残しておいて 新しい要素を得るたびにそれと同じものが残しておいた要素の中にあるかどうかを調べる

ここで残しておくのは、新しいほうは密に残しておいて、古いほうはまばらに残す

そのために、i 番目の要素は、i を 2進数で表現したときに下位に 0 がいくつ並んでいるかで 上書きする要素を決めていく

これを読んで思い出したのだが、これは昔自分でバックアップのために考えた仕掛けと同じだな

なお、下位に並んでいる 0 の数を返す関数は RULER 関数と呼ぶひとがいたらしい

#3 もっと素朴な循環小数変換

素朴なほうがいいというなら 兎と亀のアルゴリズムよりも単純に、 途中結果をぜんぶ記録しておくのはどうか

class Rational
  def to_dec_naive
    sign = self < 0 ? "-" : ""
    n = self.numerator.abs
    d = self.denominator
    int, mod = n.divmod(d)
    s = "#{sign}#{int}"
    return s if mod == 0

    f = ""
    visited = {}
    begin
      visited[mod] = visited.size
      digit, mod = (mod * 10).divmod(d)
      f << digit.to_s
      return "#{s}.#{f}" if mod == 0
    end until visited[mod]

    i = visited[mod]
    "#{s}.#{f[0,i]}(#{f[i..-1]})"
  end
end

これは、途中結果をぜんぶ記録するので、循環がなかなか見つからないと、 メモリをたくさん消費してしまう

とりあえずランダムな入力に対して to_dec_th と結果を比較して結果が一致することは確認した

で、to_dec_th と実行時間を比較

% ruby -r./recurring-decimal.rb -e '
n = 1000
puts "numerator,t,alg\n"
1.upto(n) {|i|
  n = (1.01 ** i).to_i
  d = rand(n) + 1
  r = rand(d).to_r/d
  t0 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s0 = r.to_dec_naive
  t1 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s1 = r.to_dec_th
  t2 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  raise if s0 != s1
  a = t1 - t0
  b = t2 - t1
  printf "%d,%g,naive\n", n, a
  printf "%d,%g,th\n", n, b
}
' > recurring-decimal2.csv

今回は、分母も乱数にして、あと、その乱数の範囲を指数関数的に広げて、 大きな値も測定するようにしてみた

recurring-decimal2.R:

library(ggplot2)
d <- read.csv("2020-07/recurring-decimal2.csv")
p <- ggplot(d, aes(numerator, t)) +
  geom_point(aes(colour = alg)) +
  scale_x_log10() +
  scale_y_log10("t[s]")
print(p)

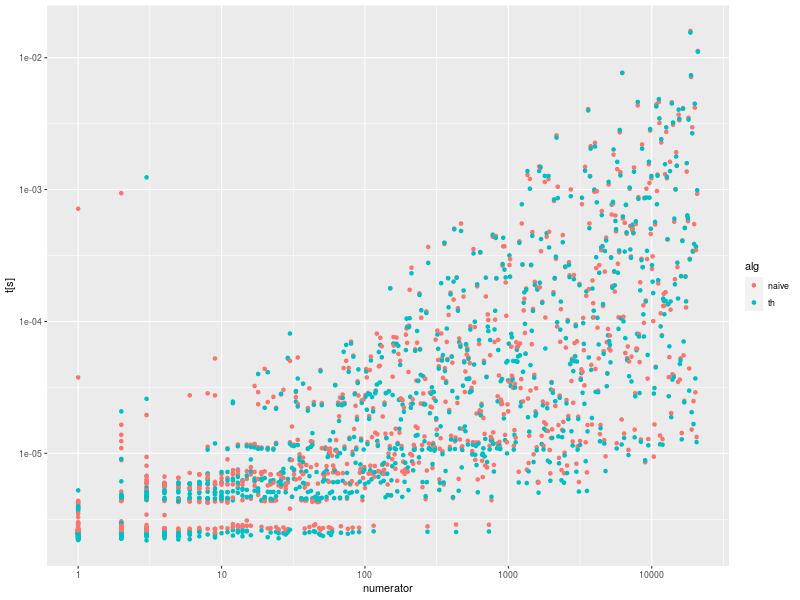
recurring-decimal2.png

まぁ、to_dec_naive と to_dec_th は速度は同じくらいかな

2020-07-19 (Sun)

#1 高速に有理数を循環小数に変換する

任意の数列に使える循環検出じゃなくて、 循環小数固有の性質を使えばもっと高速にできるのではないかと思って wikipedia の説明を読んでみた

Repeating decimal

すると、有理数 n/d に対して、d の約数の 2 と 5 を括り出して d = 2^a * 5^b * d' とすると、 繰り返されない部分の長さは max(a,b) なのだそうだ

そして繰り返し部分の長さは 10 modulo d' の multiplicative order というものになるらしい

これを使って、循環小数に変換するメソッドを書いてみた

class Rational
  def to_dec_factor
    sign = self < 0 ? "-" : ""
    n = self.numerator.abs
    d = self.denominator
    int, mod = n.divmod(d)
    s = "#{sign}#{int}"
    return s if mod == 0

    d2 = d

    # find the number of zero bits at lower bits in d.
    num_factor_2 = (d & ~(d - 1)).bit_length - 1
    d2 = d >> num_factor_2

    num_factor_5 = 0
    while d2 % 5 == 0
      num_factor_5 += 1
      d2 /= 5
    end

    h = [num_factor_2, num_factor_5].max

    if h == 0
      f = ""
    else
      digits, mod = (mod * 10**h).divmod(d)
      f = digits.to_s
      if f.length < h
        f = "0" * (h - f.length) + f
      end
    end

    return "#{s}.#{f}" if mod == 0

    # find the multiplicative order of 10 modulo d2
    l = 0
    m = 1
    begin
      m = (m * 10) % d2
      l += 1
    end until m == 1

    f << "("
    digits = (mod * 10**l) / d
    digits = digits.to_s
    if digits.length < l
      f << "0" * (l - digits.length) << digits
    else
      f << digits
    end
    f << ")"

    "#{s}.#{f}"
  end
end

例によって to_dec_th と比較して結果が一致することをテストした

データをとってプロットしてみる

% ruby -r./recurring-decimal.rb -e '
n = 1000
puts "numerator,t,alg\n"
1.upto(n) {|i|
  n = (1.01 ** i).to_i
  d = rand(n) + 1
  r = rand(d).to_r/d
  STDERR.puts [i, r].inspect
  t1 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s1 = r.to_dec_th
  t2 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  s2 = r.to_dec_factor
  t3 = Process.clock_gettime(Process::CLOCK_THREAD_CPUTIME_ID)
  raise if s1 != s2
  a = t2 - t1
  b = t3 - t2
  printf "%d,%g,th\n", n, a
  printf "%d,%g,factor\n", n, b
  STDOUT.flush
}
' > recurring-decimal3.csv

recurring-decimal3.R:

library(ggplot2)
d <- read.csv("2020-07/recurring-decimal3.csv")
p <- ggplot(d, aes(numerator, t)) +
  geom_point(aes(colour = alg)) +
  scale_x_log10() +
  scale_y_log10("t[s]")
print(p)

recurring-decimal3.png

お、なんか速くなった感じ

R の中で平均とかをとってみた

> summary(d$t[d$alg == "th"])
     Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
2.966e-06 8.672e-06 1.800e-05 2.632e-04 7.591e-05 1.666e-02
> summary(d$t[d$alg == "factor"])
     Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
2.332e-06 7.106e-06 1.073e-05 5.056e-05 2.424e-05 2.721e-03

平均が 2.632e-04 から 5.056e-05 に下がっているので、やはり速くなっている

なお、今の実装では multiplicative order は以下のように素朴に計算している

# find the multiplicative order of 10 modulo d2
l = 0
m = 1
begin
  m = (m * 10) % d2
  l += 1
end until m == 1

ただ、調べてみると、Baby-step giant-step という方法があって、もっと速くできるらしい

Baby-step giant-step

2020-07-20 (Mon)

#1 カーマイケルの定理

multiplicative order of 10 modulo d を求めるのに Baby-step giant-step で探索するよりも速いらしい方法として、 カーマイケルの定理を使うという方法があるようだ

ただ、d を素因数分解しなければならないようでギョッとする

でも、multiplicative order of 10 modulo d を素朴に計算すると、 最悪の場合、ほぼ d 回の除算が必要で、 Baby-step giant-step でも sqrt(d) 回くらいのようだ

sqrt(d) 回除算していいなら素因数分解できると思うので、 もともと素朴にやったり Baby-step giant-step でやるのが 素因数分解以上に時間がかかるということだろうな

2020-07-21 (Tue)

#1 ruby issue

Ruby Bug #17037 rounding of Rational#to_f

2020-07-29 (Wed)

#1 Coq issue

GitHub coq/issues/12771: Coq 8.12 -I option inserts ML path after user-contrib

[latest]

田中哲